歐拉常數![]()
我們知道調和級數
![]() 發散
發散
但當![]() 時,
時,
![]() 收斂到一個
0到1之間的數,我們定義為
收斂到一個
0到1之間的數,我們定義為![]() (讀gamma),也就是說
(讀gamma),也就是說
![]()
證明:
令![]() ,
則
,
則![]()
![]()
若![]() 為小於
為小於![]() 的實數,
也就是說
的實數,
也就是說
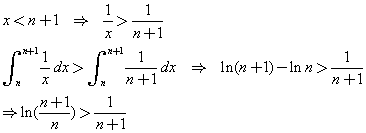
因此可以得知
![]() ,
也就是說
,
也就是說![]() 為遞減數列
為遞減數列
再假設![]()
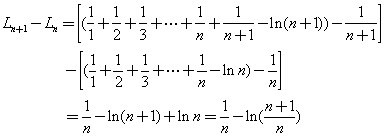
若![]() 為
大於
為
大於![]() 的實數,
也就是說
的實數,
也就是說
|
因此可以得知,
又 根據實數的完備性(completeness), |
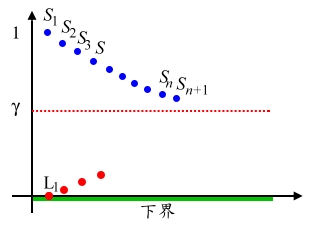 |
![]() 的近似值
的近似值
|
n值 |
|
|
10 |
0.626383161 |
|
100 |
0.582207332 |
|
1000 |
0.577715582 |
|
10000 |
0.577265664 |
|
100000 |
0.577265664 |
|
1000000 |
0.57721616 |
> evalf(sum(1/i,i=1..1000000)-ln(1000000));
0.57721616