的求法

以上題目中的無窮級數，我們在高中時期，稱之為 p 級數，我們知道 p 級數的收斂性質：當 p 大於 1時級數收斂，否之則發散。但是我們雖然知道級數收斂，那麼收斂到哪個數呢？在此，我們將 p 級數稱為   函數 (念 zeta function)，如發散 ，這是本文要討論的課題

考慮函數的根, 其根為, 我們可得到一個重要的展開式

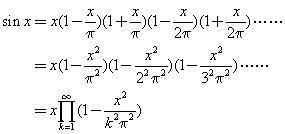
   也就是說    , 兩邊取對數

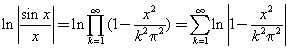
展開式1:    

展開式2:   

左:

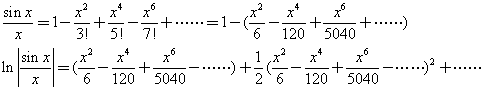
右:

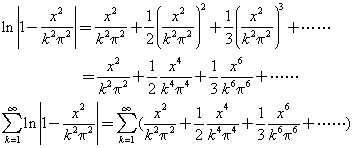
比較左與右兩者係數

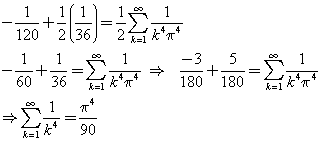
其餘的大家自行推算

註：(1)從這個等式可發現無限個有理數的和，可能變成無理數

        (2) 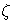  函數中偶次方的總和均可由上述等式求出

        (3) 至於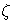  函數中奇次方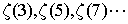，雖然知道為收斂，至今無法求出解析解，甚至是有理數還是無理數至今都尚未知悉。