自然對數的底

1.歐拉數是怎麼出現的?

2為何以歐拉數為底的指數函數，其導函數等於自己，也就是?  按這裡

3為何以歐拉數為底的對數函數，其導函數等於，也就是? 按這裡

考慮複利問題:

(a)今年初存入數學銀行100元，年利率12%，一年複利1次，明年初本利和為多少?

答:這答案大家都可以以直覺回答:112元，但最好是有以下觀念

           本利和 = 本金 + 本金˙利率

(b)今年初存入數學銀行100元，年利率12%，一年複利2次，明年初本利和為多少?

 答: 這次利息滾了2次，但利率降為一半

                半年結算成為新本金

              發現規則了嗎?

(c)今年初存入數學銀行100元，年利率12%，一年複利12次，明年初本利和為多少?

 答: 這次利息滾了12次，不需一次一次算吧!直接寫答案

(d)複利公式  :      

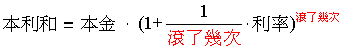
(e)由上述問題得知複利公式 ，(a),(b),(c)三種方案，何者較為有利?

問題:今年初存入數學銀行1元，年利率100%，一年複利 n次，明年初本利和為多少?

若使，為多少?

利用二項式定理

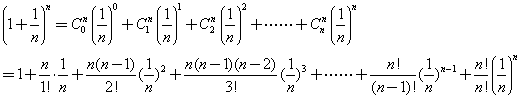
若使，

為單調增數列

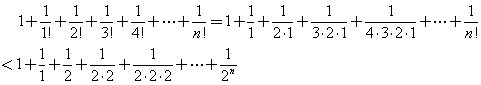
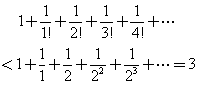
(2)有上界

(3)收斂到一個2到3之間的實數，稱為 (可能為了紀念Euler)，也就是

           其近似值